欧拉路

欧拉路径定义

通过图中所有边恰好一次且行遍所有顶点（允许多次经过同一个点）的通路称为欧拉路径。即一笔画。

如果这条路径的起点和终点重合，那么就是欧拉回路。

如何判断图是否有欧拉回路或者欧拉路径？

无向图：因为欧拉路径中，除了起点与终点以外，任意点的“进”“出”次数相等，所以除了两个点为奇点（度数为奇数的点）（终点和起点）以外，其它点的度数均为偶数。

如果是欧拉回路，奇点的个数应该为 0。

有向图：欧拉路径中，最多只有两个点的入度不等于出度。起点出度比入度大 1，终点入度比出度大 1。

如果是欧拉回路，所有点的 入度 = 出度。

Hierholzer 算法

Hierholzer 算法用于寻找欧拉回路，在找不到欧拉回路的情况下会找到欧拉路径。

算法流程：

对于无向图：

1、判断奇点数。奇点数若为 0 则任意指定起点，奇点数若为 2 则指定起点为奇点。

2、开始递归函数 Hierholzer(x):

循环寻找与 x 相连的边 x→u:

删除 x→u

删除 u→x

Hierholzer(u);

回溯时将 x 插入答案队列之中

3、倒序输出答案队列

对于有向图：

1、判断顶点入度与出度：

若所有顶点入度等于出度 → 任意指定起点；

若恰有一个顶点出度=入度 +1（起点），另一顶点入度=出度 +1（终点）→ 指定起点为前者；

其他情况 → 不存在欧拉路径/回路。

2、开始递归函数 Hierholzer(x)：

循环寻找与 x 相连的出边 x→u：

删除出边 x→u（从邻接表中移除 u）；

Hierholzer(u)；

回溯时将 x 插入答案队列之中。

3、倒序输出答案队列。

示例

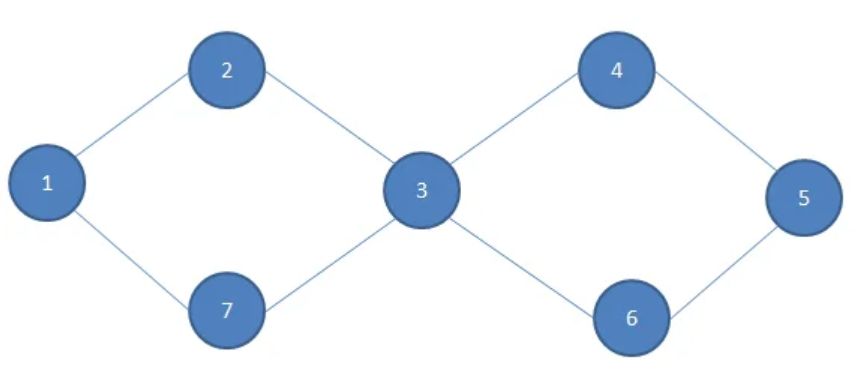
对于该图，算法的执行流程如下：

step1: 找到该图没有奇点，从 1 开始进行 Hierholzer 算法。

step2: 删边 1→2 递归到 2

step3: 删边 2→3 递归到 3

step4: 删边 3→7 递归到 7

step5: 删边 7→1 递归到 1

step6: 1 无边，1 加入队列，返回

step7: 7 加入队列，返回

step8: 删边 3→4 递归到 4

step9: 删边 4→5 递归到 5

step10: 删边 5→6 递归到 6

step11: 删边 6→3 递归到 3

step12: 3 加入队列，返回

step13: 6 加入队列，返回

step14: 5 加入队列，返回

step15: 4 加入队列，返回

step16: 3 加入队列，返回

step17: 2 加入队列，返回

step18: 1 加入队列，返回

答案队列为：1 7 3 6 5 4 3 2 1。反向输出即为答案。

示例代码

#include<bits/stdc++.h> //万能头文件
using namespace std;

struct node{
	int u;
	bool vis;  //记录是否被访问过
};
int n,m; 

vector<node> v[100010];
int in[100010],st[100010]; //in 表示每个结点入度与出度的差（即入读 - 出度）

stack<int> s;  //记录答案

void dfs(int x){
	for(int i=0;i<v[x].size();i=max(i+1,st[x])){
		if(v[x][i].vis) continue;
		v[x][i].vis=1;
		st[x]=i+1;
		dfs(v[x][i].u);
	}
	s.push(x);
}

bool cmp(node a,node b){
	return a.u<b.u;
}

int main(){

	cin>>n>>m;
	for(int i=1,x,y;i<=m;i++){
		cin>>x>>y;
		v[x].push_back(node{y,0});
		in[y]++;
		in[x]--;
	}
    
	int fb=0,fe=0,pb=1,pe; 
	for(int i=1;i<=n;i++){  //判断是否存在欧拉路径
		if(in[i]>1||in[i]<-1) {
			printf("No");
			return 0;
		}
		if(in[i]==1) fe++,pe=i;
		if(in[i]==-1) fb++,pb=i;
		if(fb>1||fe>1) {
			printf("No");
			return 0;
		}
	}
    
	for(int i=1;i<=n;i++) sort(v[i].begin(),v[i].end(),cmp);
    
	dfs(pb);
    
	while(s.size()){
		printf("%d ",s.top());
		s.pop();
	}
	return 0;
}

例题：